Prof. E. Colman
Written: 1931;
Source: Science at the Crossroads:
Papers Presented to the International Congress of the History of Science and technology Held in London from June 29th to July 3rd, 1931 by the delegates of the U.S.S.R, Frank Cass and Co., 1931;
Online Version: For marxists.org May, 2002.
The position of mathematics, as that of any science, is at bottom determined by the development and the position of the forces of production, of technology and economy. The latter affect mathematics both directly, by presenting it with new problems, creating its material basis and supplying its man-power, and indirectly through the prevailing outlook upon the world, the philosophy of the ruling class.
Thus, if we wish to deal with the present crisis in the mathematical sciences, we must take into consideration the crisis in bourgeois science as a whole, the crisis in the bourgeois natural sciences, and particularly in physics. The present paper, however, lays no claim to illuminate fully this aspect of the problem presented, the connection between the crisis in mathematics and the general crisis in bourgeois science, as well as its connection with the entire crisis within capitalism as a whole. It suffices to indicate that the crisis which is at the present time disturbing the whole of bourgeois science represents a new and higher phase of that crisis, experienced by physics and chemistry since the opening of the twentieth century, which Lenin analysed with the mind of a genius in his work, published in 1908--Materialism and Empirio-Criticism.
Of the relevant entire complex of problems, one is of special interest to us to-day: the crisis in mathematics taken in itself. Its significance is extremely great; for there is no doubt that, as the crisis in the natural sciences affects mathematics, so the crisis in mathematics, in its turn, exercises influence upon physics, chemistry and technology. On the position of mathematics, on its capacity to solve this or that problem, depends to a large extent the possibility of further development of the natural sciences and technology.
This applies with particular force to present-day physics, with its remarkably abundant mathematical apparatus, with its efforts to formalise physics, to geometricise it, its aim of allowing matter to disappear and of retaining equations only--the tendencies so strikingly revealed by Lenin. The mathematicisation of physics frightens the physicist himself; thus, for example, speaking of mathematics in physics, Khvolson says: "The most terrible thing is, that this mathematics is not the mathematics taught at the university. Not a single physicist has ever heard anything of the latter. The most terrible thing is, that its importance is continually growing." And although we oppose such obscurantism, we must admit that physics is becoming more and more dependent upon the fate of mathematics.
It is extremely characteristic that this special mathematics--the tenser analysis, the matrix calculus, the theory of characteristic numbers, has for the greater part been created by the physicists themselves, for ordinary mathematics is unable to satisfy the requirements of present-day physics.
Analysis, the most powerful instrument of mathematics, developed on the soil provided by the natural sciences, the physics, and mechanics of the 17th, 18th and 19th centuries; that is to say, on the continuity principle "natura non facit saltus." Mechanics and phenomenological thermodynamics regarded all processes as continuous (at least at a first approximation), and expressed them analytically. The same was true of electro-magnetism and even of chemistry.
Nevertheless, a number of discoveries were forced upon this "harmony of continuity," which, beginning with Planck's energy-quantum that was necessary to explain the heat radiation of a black body, develops through light-quanta and photons to the wave mechanics of de Broglie, Heisenberg and Schrodinger. Physics could provide no consistent analytic explanation of these phenomena and all attempts to establish a synthesis of waves and atoms, of electro-magnetism and gravitation, have so far failed, or at best, have resulted merely in ad hoc hypotheses. Thus, for example, Dirac's unitary theory of electricity, which is compelled to introduce the conception of negative energy, only confirms anew the contention that dialectics, which is forcing its way into science with elemental power, becomes a caricature of itself in the hands of idealist physicists. Still less working capacity is displayed by mathematics, which is scarcely able to solve the equations of wave mechanics in the most simple and trivial instances.
This inability to present an adequate picture of material reality--i.e., of the world existing independently of our consciousness--is exhibited on analysis even in comparatively elementary instances.
Let us take, for example, such a problem as that of cooling a rod, one that will appear quite simple to anybody who has not yet been corrupted by school physics and mathematics. It is well known, however, that the solution of the relevant partial differential equation with its relevant boundary conditions is of import only if we have found a series of discrete values of a parameter. Thus in itself the continuous solution of the partial differential equation does not help to elucidate the physical nature of the phenomenon. Assistance is offered by a discontinuous series of numbers and the solution breaks through the bounds of continuity.
We find similar circumstances in problems which are connected with the equilibrium of films (Plateau) and with the entire group of problems in which the given set of circumstances is dependent upon all preceding circumstances, that is, whenever we encounter integral equations, in numerous problems of variation, etc. It is obvious that this consisting of two wholly separate branches, along which analysis is compelled to seek a way out--first by continuous solutions, and secondly, by discrete values--can be regarded only as provisional and palliative. It is obvious that new paths must be sought.
And indeed mathematicians are trying to find a new road, but not in the right direction. As opposed to analysis, which is based upon the idea of continuity, the first quarter of our century has witnessed the vigorous development of that branch of mathematics which assigns first place to the idea of discontinuity as being self-sufficient--the theory of manifolds, the theory of real functions and, in most complete form, the theory of analytic manifolds.
Not to go too far afield, we would refer to the book by the academician Lusin (Moscow) published in Paris in 1930: Lecons sur les ensembles analytiques et leurs applications. The main principle depends on the formation of what is called Bair's fundamental domain. All points with rational co-ordinates are excluded from the continuum, only those points remaining which possess irrational co-ordinates; these form the fundamental domain and various operations are undertaken with them. This gives us an absolute discontinuity, for in however small a domain of any point of discontinuity you may choose, there are as many points of discontinuity of the original continuum. The question arises: where is there in material nature anything for which such an absolute discontinuity would be adequate? We find an unexpected answer to this difficult question in Lebesque's introduction to the book mentioned above: in his opinion the philosophical value of this work is even greater than its mathematical value, for its standpoint is the standpoint of solipsism. It is not difficult to understand that analytic manifolds which are built up on the concept of absolute discontinuity reflect with remarkable fidelity the extreme individualism of idealist philosophy.
We are thus presented with two extremes: continuity transformed into the absolute and the discrete made absolute, both laying claim to independent and sole significance, neither seeking reciprocal unity, each giving a one-sided picture of material reality. Consequently, the problem is not solved by rejecting both analysis and discrete mathematics as irregular and contrary to law, by dismissing both without further ado in order to start constructing afresh on clear ground; the solution lies in creating a new manner of calculation which, proceeding from a uniform principle, unites in itself the positive sides both of analysis and discrete mathematics.
The method of creating an external supplement--of discrete mathematics--to analysis, is therefore incapable of giving the synthesis of continuity and discontinuity; it is unable to lead mathematics out of its present position, in which functions containing discontinuities are treated as "unreasonable," in which gaps are considered as regrettable and undesirable revolutionary exceptions; or, on the other hand, in which the discrete is made absolute and regarded as the set of isolated individuums. We need not two analyses, but one, which in its operations would reflect the unity of continuous and discontinuous. But for such unity to be established mathematics must become dialectical and mathematicians must not fight shy of dialectical materialism.
The attempts to overcome the crisis in the present position of mathematics, which is unable to offer a synthesis of continuum and discontinuum because it is in the hands of metaphysical mathematicians, may also be described as attempts to arithmeticise analysis. The attempts are made with unsuitable means. Kronecker's old call: "Back to arithmetic!" is just as reactionary as the modern cry to let physics turn back to magic, chemistry to alchemy, and medicine to Hippocrates. We have not to arithmeticise analysis, but to introduce a new quality and bridge the gulf between continuity and discontinuity.
Apart from this gulf, however, we cannot but call attention to a second, and that is the breach between mathematics as a whole and the calculation of probability, one that is of particular importance in relation to the role of statistics in present-day physics, biology, etc.
The calculation of probability, it is well known, makes use of all branches of mathematics: arithmetic, algebra and analysis, but it is not in this that its profound connection with mathematics as a whole lies.
By the theory of geometrical probability it is known that it is possible to ascertain experimentally the value of the number π by throwing a needle upon a quadratically ruled surface and counting the number of instances in which the lines are cut by the needle, as Buffon showed in 1777 in his Essai d'arithmetque morale, and as has been practically demonstrated by Wolff in Zurich.
Of the same character as this problem, in which it is possible, by a large number of experiments, to determine with a small margin of error exact mathematical magnitudes, are the well-known urn problems, such as determining the probability that, in drawing an even number of balls out of an urn containing an equal number of black and white balls, the black and white balls will appear in equal numbers, in which the expression of probability contains the square root of a π. Or, as another example, the determination of the probability that, in drawing numbered balls singly out of an urn, the number of the ball drawn will not once coincide with the serial number, which gives a probability of i/e in the case where the number of balls exceeds all limits. It may appear even more surprising that the calculation of probability enables us to find algebraic and arithmetic relations, often extremely complex. Thus, for example, Moivre's well-known problem, given in his work "De mensura sortis seu de probabilitate eventuum in ludis a casu fortuito pendetibus," published in 1711, which consists in finding the probability that, in drawing numbered balls, the total of the numbers will equal a number previously given, leads to the relation:
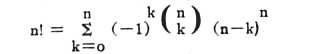
Or, let us taken another example, quite elementary but extremely important methodologically: the summing up of a geometrical series by means of a probability procedure; this example at the same time propounds the problem of finding stochastic schemes that will enable even more complex convergent series to be added up. Finally we would also point out that the calculation of probability enables us to ascertain with sufficient accuracy such irrationals as √ 2 as indicated in the same connection, by Professor Khotimsky (Moscow). Actually, if we grant a margin of error of 0.5 we arrive at 2 √ 2 = √ 8 = 3, 5 √ 2 = √ 50 = 7, 7 √ 2 = √ 98 = 10 from which it follows, on the theory of errors, that
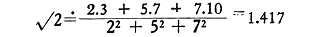
The general problem of determining with the desired accuracy the roots of an equation by stochastic methods can be put in analogous fashion.
The question arises how such results are possible. How is it possible that a calculation based upon chance can give exact laws, can lead to the most exact results? This question is not answered by present-day mathematics: it does not study these relations but regards them rather as a sort of curiosity, or mystery, and it is quite incapable of explaining them, because its metaphysical mode of thought is unable to grasp the unity of statistical and dynamic regularity, considering them as existing separately and antagonistically. This circumstance is, however, not only of philosophical significance; it means that present-day statistical theory is at a standstill, that the law of large numbers is not developed in the direction of varying processes. All this, in its turn, is connected with the fact that mathematics developed principally upon the basis of the natural sciences and is entirely unsuited to serve the needs of scientific political economy. It is not difficult to understand why all attempts to establish, along purely formal lines, a correspondence between the elements of the calculation of probability and of analysis have been barren of result.
The third, still broader and more profound gulf in present-day mathematics lies in the extreme lack of quality in most of its methods. By lack of quality in mathematics we do not mean, of course, that mathematical concepts have only to represent repetitions of a few main concepts, their quantitive complications. In remaining a science of magnitude, mathematics creates in magnitude itself its own specific mathematical qualities. Indeed, it develops as a whole from quantity to mass, from the abstract to the concrete and receives new content from the influence of physics and the natural sciences generally. Nevertheless, this development is extremely contradictory: in the separate branches of mathematics it often proceeds from the concrete to greater and greater abstraction, more and more eliminating quantitative factors. An excellent example is offered by the non-Euclidean geometries. While, actually, their origin reflects a more profound knowledge of reality, in bourgeois mathematics the fact of their existence is used as conclusive evidence of the correctness of idealism and even their mathematical treatment suffers idealist distortion. In this way, that which actually forms the cognitive power of mathematics, its colossal power of abstraction at certain stages of its development, is transformed into its own contradiction and makes mathematics of a given social formation incapable of dealing with the more complicated problems that arise as our physical knowledge penetrates deeper into the profundity of matter. And even if we are not able radically to change the nature of the object of mathematics, since, on the contrary, this object determines the content of mathematics, still we must develop mathematics further in the direction of rendering more precise the qualitative variations in the sphere of quantity itself.
Mathematics reflects real dependence as functional dependence; that is to say that even the most simple dependence, the causal, is here portrayed in the most distorted, irrelevant manner; still less can mathematics portray such dependence as interaction and the unity of mutually interpenetrating contradictions. Mathematical equations have no direction, while equations which are not divested of the qualitative properties of reality--whether they are equations of the value-form in political economy, or chemical equations--possess direction by their very nature. In "Capital" Marx refers to the polarity of the simple value-form, in which the expression
20 ells of linen equals 1 coat
cannot be simply transposed into
1 coat equals 20 ells of linen.
The irreversability of chemical equations, which are exothermic in one direction and endothermic in the other, is generally known. The question then arises, why mathematical symbols, and operations with them, could not approach to many of those qualitative peculiarities of which mathematics would otherwise make abstractions. This way of putting the question, however, has nothing in common with the attempts to mathematicise all and sundry laws, nothing in common with the attempts to give a pan-mathematical picture of the world, attempts that rely upon Pythagoreanism and cabbalistics. The object of mathematics has limits, just like the object of physics, chemistry, biology or political economy. Just as the laws of political economy cannot be investigated by biology or physics, just as physics and chemistry are unable to elucidate biological laws, so mathematics will never be in a position to replace physics, chemistry, etc. Even if mathematics, geometry, mechanics, physics, chemistry, biology, etc., have this much in common, that they all treat of the laws of the different forms of movement of matter, and while, for example, physics and chemistry on the one hand and biology on the other cannot be regarded as so sharply separated from each other as the vitalists would have us believe, dialectical materialism does not adopt the standpoint of naive mechanistic materialism, which would reduce biology to chemistry and physics, these to mechanics and the latter to geometry and mathematics. Unity implies identity just as little as difference implies separation. Retaining its specificum and without laying claim to being a panacea, mathematics can and must, at a certain stage of its development on to a higher basis, turn back to its starting point, to greater concreteness, to a greater concern with quality.
This sort of attempt has already been made with success. Thus, for example, both magnitude and direction figure in the vector analysis, whose origin and development is closely bound up with the history of mechanics and electro-mechanics. Why should we not proceed further along this road and attempt to create a new qualitative calculus, for example, for the purposes of any given branch of physics? Why should we not in this way try to put into operation the grain of truth that is contained in the idealist confusion of Leibnitz, that is, to create a calculus which would be able "to represent figures and even machines and movements by letters, just as algebra represents numbers and magnitudes." (Letter from Leibnitz to Huyghens, 1679.) But to accomplish such a change in mathematics it is necessary for mathematicians to realise the true connection between concrete and abstract, to dissociate themselves from the attitude which makes a fetish of mathematics, from the idealist and non-dialectic conception of the relation between mathematics and reality.
The fourth main gulf in present-day mathematics is that between the historical and the logical. Mathematics raises problems, operates with concepts and methods that are, obviously, historically necessary, that are conditioned by the whole development of technology, the natural sciences, philosophy, and mathematics itself. But in mathematics itself, as a system of science, this historical necessity is not directly reflected. Let us take as an example the development of such a fundamental concept as that of number.
At present mathematics develops this concept on the basis, either of the so-called Hankelian permanency principle, or of Hilbert's axiomatic principle. But the permanency principle is never realised--the development of number breaks through it. As for Hilbert's axiomatics, it is true that it is of use in explaining the logical connections between individual mathematical concepts, but, since it represents a construction post factum it, too, is unable to give a correct picture of development. Thus, in fact, both principles only obscure the historical development that has really taken place.
We would give as a further example such an elementary fundamental expression as
It is well known that this expression was not artificially invented; it arose from the historical requirements of overseas trade, from the need to create, for practical calculations, the most suitable logarithmic tables. Therefore the answer to the question why this limit e and no other is dealt with, is given not by mathematics, but by history. Nevertheless there is some point in seeking the logical reasons for which we study precisely this limiting expression. We can also arrive at the same question by another road: we require analogous limiting expressions to be constructed, so that the number e is included as a link in such a series. Of course, the problem is not unambiguous, but if there were such a series it would offer us the possibility of obtaining a fuller understanding of the number e. Hilbert actually approaches this problem from another aspect: in the 12th point of his Paris Programme he propounds the problem of finding functions that would play the same part in any algebraic body as the exponential function plays for the body of rational numbers.
Since, in the present-day system of mathematics, there are no logical reasons why any given subject is dealt with, it seems to anybody who is not familiar with the history of mathematics that all new ideas and all new problems appear in mathematics sporadically, and to put forward problems such as those mentioned above causes confusion among mathematicians, for mathematics in its present position offers no clues to their solution. This circumstance is favourable to idealism, to fideism, by making it appear that it is a question of the free creation of the immanent understanding, of inspiration, and at the same time it demonstrates the incapacity of mathematics to-day to provide far-reaching generalisations that would give it a powerful impulse forward, embrace all its branches, eliminate the existing parallelism and remove from it superfluous geological stratifications. If this is to be done, the gulf between the historical and the logical in mathematics structure, methods and problematics must be revised in the light of the unity of the historical and the logical.
The fifth gulf in mathematics exists between theory and practice in mathematics itself. While mathematical theory is extremely ramified and develops very rapidly and luxuriantly, mathematical practice, that is, the methods of calculation, scarcely moves forward at all; indeed, it has practically remained stationary at the position it occupied in the 17th and 18th centuries. In actual fact, every mathematical problem, if it is to have any significance at all in practice, must eventually lead to some process of calculation, the solution which mathematical theory offers us must be effective. As it is, however, the greater part of mathematics, and particularly the more recent, gives us no effective results and scarcely troubles to do so, concerning itself rather with logical "proofs of existence."
The methods of calculation we use can in essence be traced back to the logarithms which Newton used. A large number of mathematical methods, powerful in theory, are proved in practice to be useless because the forms of their application have not been worked out. These include all self-developing processes as, for example, convergent series, products, continued fractions, iterations, recurrent processes, whose slow convergence makes them for the most part useless. Since, in present-day mathematics as in bourgeois science as a whole, "pure" mathematics is kept wholly apart from applied mathematics, the question of methods of calculation, instruments and tables that would enable whole categories of convergent series of a given type to be summed up with the required accuracy--to take one example--is not even raised, and in any case "pure" mathematics consider that it has no bearing upon their divine science. Nevertheless, the creation of such instruments would give us new logarithms which would enable us to tackle much more complicated problems than we can at present, when we are compelled to consider a problem as solved only when it leads to the main arithmetical operations. In this way the problem of reduction would be placed in quite a new light. But in order to bridge the gulf between the colossal theory and the comparatively small effectiveness of mathematics, it is essential to have a really scientific understanding of the unity of theory and practice, an understanding of the primacy of practice over theory which bourgeois mathematics to-day do not, and cannot possess.
The sixth gulf is that which exists in the so-called foundation of mathematics or, more exactly, in that philosophical superstructure whose purpose it is to justify the whole edifice, to incorporate it in the world system as a whole. The two rival philosophies for present-day bourgeois mathematics, the logistic and the intuitionist, are both idealist. It is a matter of indifference whether the world of mathematical concepts is regarded as a world of rigid immovable universals, as it is by the logists, or whether it is looked upon as the sphere of action of the free becoming as it is by the intuitionists. It is just the same if one agrees with Russell that mathematical concepts are a priori reducible to the natural series which is given complete in its infinite totality, or if one assumes with Weyl that mathematical concepts are born intuitively, not from sense-perception and comprehension, but in some mystic fashion apart from being. The one philosophy, just as little as the other, is able to resolve the paradoxes of the manifold theory, the law of the excluded middle, the contradiction between the singular and the many, and the finite and the infinite. The most refined finesses of finitism, of metalogic, of mathematical atomistics, merely express the anxiety of bourgeois mathematicians to separate themselves from matter and dialectics by the veil of formal logic, guiding them directly into the desert of scholasticism.
All the profound contradictions of mathematics--the contradiction between the singular and the manifold, between the finite and the infinite, the discrete and the continuous, the accidental and the necessary, the abstract and the concrete, the historical and the logical, the contradiction between theory and practice, between mathematics itself and its logical foundation--all are in reality dialectical contradictions. Their mutual inter-penetration and struggle really embody the development of mathematics. But because of the absence of plan in tackling these problems, because anarchy reigns in bourgeois mathematics as it does throughout bourgeois science as a whole and the entire capitalist system, because there is not and cannot be any general planning, the process of mathematical development encounters severe crises, experiences periods of stagnation and decline. This is reinforced by the influence of the idealist, metaphysical class philosophy and by the extreme division of labour characteristic of the whole of capitalist society and which is particularly evident in mathematics, where it is difficult to find a scientist able to understand scientific works that do not come within his own narrow province.
For mathematics there is only one way out: conscious, planned reconstruction on the basis of materialist dialectics. Is it, however, at all possible to speak of the deliberate reconstruction of mathematics and science as a whole, of the introduction of planning into science, into mathematics? The old prejudice about what is called the creative scientific work of the individual, arising from inspiration, has been destroyed by the development of science itself. There have always been scientific schools, and the creative work of one individual is rooted firmly in the collective work of the whole. And as far as planning is concerned, under capitalism the great trusts establish magnificent research institutes organised for collective work. In any case, the history of mathematics itself answers this question in the affirmative. Klein's Erlanger Programme will serve as an example; this programme, put forward in 1872, when German capitalism was growing and flourishing, accomplished a real revolution in geometry. It has had extremely fruitful results and is remarkable in that it is based upon a uniform idea, the group idea, the idea of a group of spatial transformations and of discovering the invariables which characterise it. The programme put forward by Hilbert in 1900 has been much less successful than the Erlanger Programme; it is not founded upon a uniform idea and is rather an index of separate problems--happily grasped, it is true--from all branches of mathematics. Consequently it did not accomplish in mathematics the revolution that Klein's programme did in geometry, although, despite its mosaic character, it played a positive part in directing the attention of the younger mathematicians to apparently insoluble problems--among others, Gelfond (Moscow) and Shnirelman (Moscow).
The Erlanger programme was so successful because it is not a mathematical, but a geometrical programme. Geometry, as a science that is more material than mathematics, has not only detached itself less from reality than the latter, but has frequently been of assistance to it. Geometrical methods and problems have had a wholesome effect upon mathematics by drawing it back to "A sinful mother earth."
This does not imply, however, that geometry ever had more than an auxiliary part to play, that it was ever in the position to assume the leading part of the general abstract form that algebra plays in mathematics, that it could ever give more than the intuitive perception which it does give. This, too, is the standpoint from which we have to consider the most recent branch of geometry, topology, which studies the most general qualities of spatial structures that remain unchanged by any continuous uni-univalent transformations. From topology, in which a certain synthesis of the constant and the variable (group theory topology and manifold theory topology) has already been achieved and in which the school of Alexandrov, Pontriagin (Moscow) and others is making conscious efforts to give logical foundation to the fact that topological problems have been raised, a number of methods were worked out providing a solution for mathematical problems that have to be comprehended synthetically: these are the topological methods of Lusternik and Shnirelman as applied to the calculation of variations. It is to be hoped that the study of topological methods will indirectly help mathematics to progress further along this road.
If the problems enumerated above are to be solved, how is one to begin with the plan of reconstructing mathematics? The most simple thing, of course, would be if somebody should come forward with a ready-made plan, but that would be a sentence of death on the plan itself, for to-day, since mathematics has so many branches, the plan that we want can only be drawn up by collective work. Such a plan, which can be made only in a country where the national economy and science are planned, must be drawn up on the basis of all the experience gained in scientific research institutes and works' laboratories, on the basis of the requirements of the industry, agriculture and transport of the whole country. It should, however, be more than a mere register of themes suggested at conferences by scientists and engineers; it must arise as the result of intensive work on the material thus collected and its foundation must be supplied by materialist dialectics.
Hence it follows that we cannot overlook whatever has a bearing upon mathematics and its history in the writings of Marx, Engels, and Lenin. We should carefully study everything on this subject in Engels' "Anti-Duhring" and "Naturdialektik," in Lenin's "Materialism and Empirio-Criticism," in his philosophical writings and in a number of other works, particularly the economic. The hitherto unpublished writings of Marx dealing with mathematics and its history, of which there are more than fifty and which will shortly be published by the Marx-Engels Institute (Moscow), are of tremendous methodological importance.
The history of the mathematical sciences must be studied in the light of Marxist-Leninist theory, of the philosophy of dialectical materialism and the question of the tendencies in their development worked out in full detail. Above all we have to study the development of mathematics in the epoch of imperialism and the proletarian revolution, to continue upon a dialectical-materialist basis the work of Klein, the most advanced of bourgeois mathematicians, in whose works we discover, besides Machism, essential constituents of spontaneous materialism. The work of bringing out such a volume is now in progress. We have to concentrate our attention upon the development of the main mathematical concepts, particularly upon such important concepts as the differential quotient, the differential, the limiting concept. We must make a really scientific classification of the mathematical sciences; we have to investigate the importance of algebra as a connecting link between arithmetic and analysis, to study such "neglected" branches of mathematics as, for example, equations of finite differences and their connection with analysis, or divergent series; we have to find out why for the time being mathematics has turned away from them, we have to determine the position of the theory of numbers in mathematics, to study its development and the development of the entire structure of the mathematical sciences.
In addition to all these general theoretical problems there are a number of others, directly connected with socialist construction in the Soviet Union, which can be embodied into a programme of practical work for Soviet mathematicians.
We are now considering the organisation of a calculation institute for the entire Soviet Union, whose task it will be to work out new methods of calculation, to solve the mathematical problems that arise in our socialist industry, in the transport system, in collectivised and industrialised agriculture; this institute will become the operative staff for ail mathematical work being conducted by the different scientific research institutions throughout the country.
One group of problems which our mathematicians have to solve is presented by the statistical problems that are so important in planned socialist economy, questions of designing and distributing economic centres (whose great importance was emphasised by Lenin), of rationalising the transport of goods, etc.
A second group is concerned with the standardisation of production, with working out optimal forms and series of products, with the problems of transmission belts and dies that arise in the rationalisation of undertakings.
The third group consists of problems that have arisen in working out the best topographical and cartographical methods corresponding to the rate of socialist construction; this is of colossal importance in a country such as the Soviet Union, with its vast natural wealth that remained uninvestigated under the predatory capitalist economy of tsarism.
There is also a fourth group of less comprehensive problems connected with the statistics of the earth's interior, with the rapidly developing building industry, the construction of airships, etc.
It is only planned socialist economy that can present mathematics with such problems, demanding the complex participation of various branches of mathematics (e.g., calculation of probability combined with differential geometry, calculation of probability and calculation of variation, or calculation of variation and the theory of numbers, etc., complex mathematical problems adjusted to mathematical mass production and maximum effectiveness, together with extensive scientific work of theoretical Investigation. Thus, to plan mathematics does not mean to stifle creative work--it means that mathematics will flourish as it can do only with collective labour, the more so as the ranks of the scientists are swelled by new men from the working class, to whom the gates of the universities and research institutes have been opened wide.
The important question of reorganising the teaching of mathematics at all stages of education, from the polytechnic to the university, cannot be dealt with here.
To solve all these theoretical and practical problems, to overcome the crisis in present-day mathematics, to reconstruct it along socialist lines, patient and persistent work is necessary, the collective work of all Soviet mathematicians and of those scientists in capitalist countries who wish to go with us. Proceeding from the Leninist theory of the unity of theory and practice, we in the Soviet Union shall reconstruct the mathematical sciences. Acknowledging the Leninist principle that the sciences are not impartial, we shall place mathematics at the service of socialist construction and in this wav save it from the decay that is inescapable under capitalism.